Probabilistic logics in machine learning
Fabrizio Riguzzi
University of Ferrara
http://ds.ing.unife.it/~friguzzi/PLML-ECML/
http://cplint.lamping.unife.it

Outline
Logic
Probabilistic logics
Probabilistic logic programming
Applications
Inference
Learning
Examples
Logic
Useful to model domains with complex relationships among entities
Various forms:
First Order Logic
Logic Programming
Description Logics
First Order Logic
Very expressive
Open World Assumption
Undecidable
\[\begin{array}{l} \forall x\ Intelligent(x)\rightarrow GoodMarks(x)\\ \forall x,y\ Friends(x,y)\rightarrow (Intelligent(x)\leftrightarrow Intelligent(y)) \end{array}\]
Logic Programming
A subset of First Order Logic
Closed World Assumption
Turing complete
Prolog
\[\begin{array}{l} \mathit{flu}(bob).\\ hay\_\mathit{fever}(bob).\\ sneezing(X)\leftarrow \mathit{flu}(X).\\ sneezing(X)\leftarrow hay\_\mathit{fever}(X).\\ \end{array}\]
Description Logics
Subsets of First Order Logic
Open World Assumption
Decidable, efficient inference
Special syntax using concepts (unary predicates) and roles (binary predicates)
\[\begin{aligned} &&{\mathit{fluffy}}: Cat\\ &&tom : Cat \\ &&Cat \sqsubseteq Pet \\ &&\exists hasAnimal.Pet \sqsubseteq NatureLover\\ &&(kevin, {\mathit{fluffy}}):hasAnimal \\ &&(kevin, tom):hasAnimal \end{aligned}\]
Combining Logic and Probability
Logic does not handle well uncertainty
Graphical models do not handle well relationships among entities
Solution: combine the two
Many approaches proposed in the areas of Logic Programming, Uncertainty in AI, Machine Learning, Databases, Knowledge Representation
Probabilistic Logic Programming
Distribution Semantics [Sato ICLP95]
A probabilistic logic program defines a probability distribution over normal logic programs (called instances or possible worlds or simply worlds)
The distribution is extended to a joint distribution over worlds and interpretations (or queries)
The probability of a query is obtained from this distribution
Probabilistic Logic Programming (PLP) Languages under the Distribution Semantics
Probabilistic Logic Programs [Dantsin RCLP91]
Probabilistic Horn Abduction [Poole NGC93], Independent Choice Logic (ICL) [Poole AI97]
PRISM [Sato ICLP95]
Logic Programs with Annotated Disjunctions (LPADs) [Vennekens et al. ICLP04]
ProbLog [De Raedt et al. IJCAI07]
They differ in the way they define the distribution over logic programs
PRISM
\[\begin{array}{l} sneezing(X)\leftarrow \mathit{flu}(X), msw(\mathit{flu}\_sneezing(X),1).\\ sneezing(X)\leftarrow hay\_\mathit{fever}(X),msw(hay\_\mathit{fever}\_sneezing(X),1).\\ \mathit{flu}(bob).\\ hay\_\mathit{fever}(bob).\\ \\ values(\mathit{flu}\_sneezing(\_X),[1,0]).\\ values(hay\_\mathit{fever}\_sneezing(\_X),[1,0]).\\ :- set\_sw(\mathit{flu}\_sneezing(\_X),[0.7,0.3]).\\ :- set\_sw(hay\_\mathit{fever}\_sneezing(\_X),[0.8,0.2]). \end{array}\]
Distributions over \(msw\) facts (random switches)
Worlds obtained by selecting one value for every grounding of each \(msw\) statement
Logic Programs with Annotated Disjunctions
\[\begin{array}{l} sneezing(X):0.7\vee null:0.3\leftarrow \mathit{flu}(X).\\ sneezing(X):0.8\vee null:0.2\leftarrow hay\_\mathit{fever}(X).\\ \mathit{flu}(bob).\\ hay\_\mathit{fever}(bob).\\ \end{array}\]
Distributions over the head of rules
\(null\) does not appear in the body of any rule
Worlds obtained by selecting one atom from the head of every grounding of each clause
ProbLog
\[\begin{array}{l} sneezing(X)\leftarrow \mathit{flu}(X),\mathit{flu}\_sneezing(X).\\ sneezing(X)\leftarrow hay\_\mathit{fever}(X),hay\_\mathit{fever}\_sneezing(X).\\ \mathit{flu}(bob).\\ hay\_\mathit{fever}(bob).\\ 0.7::\mathit{flu}\_sneezing(X).\\ 0.8::hay\_\mathit{fever}\_sneezing(X).\\ \end{array}\]
Distributions over facts
Worlds obtained by selecting or not every grounding of each probabilistic fact
Distribution Semantics
Case of no function symbols: finite Herbrand universe, finite set of groundings of each switch/clause
Atomic choice: selection of the \(i\)-th atom for grounding \(C\theta\) of switch/clause \(C\)
represented with the triple \((C,\theta,i)\)
a ProbLog fact \(p::F\) is interpreted as \(F:p\vee null:1-p.\)
Example \(C_1=sneezing(X):0.7\vee null:0.3\leftarrow \mathit{flu}(X).\), \((C_1,\{X/bob\},1)\)
Composite choice \(\kappa\): consistent set of atomic choices
The probability of composite choice \(\kappa\) is \[P(\kappa)=\prod_{(C,\theta,i)\in \kappa}P_0(C,i)\]
Distribution Semantics
Selection \(\sigma\): a total composite choice (one atomic choice for every grounding of each clause)
A selection \(\sigma\) identifies a logic program \(w_\sigma\) called world
The probability of \(w_\sigma\) is \(P(w_\sigma)=P(\sigma)=\prod_{(C,\theta,i)\in \sigma}P_0(C,i)\)
Finite set of worlds: \(W_T=\{w_1,\ldots,w_m\}\)
\(P(w)\) distribution over worlds: \(\sum_{w\in W_T}P(w)=1\)
Distribution Semantics
Ground query \(Q\)
\(P(Q|w)=1\) if \(Q\) is true in \(w\) and 0 otherwise
\(P(Q)=\sum_{w}P(Q,w)=\sum_{w}P(Q|w)P(w)=\sum_{w\models Q}P(w)\)
Example Program (LPAD) Worlds
\[\begin{array}{ll} sneezing(bob)\leftarrow \mathit{flu}(bob).& null\leftarrow \mathit{flu}(bob).\\ sneezing(bob)\leftarrow hay\_\mathit{fever}(bob).& sneezing(bob)\leftarrow hay\_\mathit{fever}(bob).\\ \mathit{flu}(bob).&\mathit{flu}(bob).\\ hay\_\mathit{fever}(bob).&hay\_\mathit{fever}(bob).\\ P(w_1)=0.7\times 0.8 &P(w_2)=0.3\times 0.8\\ \\ sneezing(bob)\leftarrow \mathit{flu}(bob).& null\leftarrow \mathit{flu}(bob).\\ null\leftarrow hay\_\mathit{fever}(bob).& null\leftarrow hay\_\mathit{fever}(bob).\\ \mathit{flu}(bob).&\mathit{flu}(bob).\\ hay\_\mathit{fever}(bob). &hay\_\mathit{fever}(bob).\\ P(w_3)=0.7\times 0.2 &P(w_4)=0.3\times 0.2 \end{array}\] \[\label{ds} P(Q)=\sum_{w\in W_\mathcal{T}}P(Q,w)=\sum_{w \in W_\mathcal{T}}P(Q|w)P(w)=\sum_{w\in W_\mathcal{T}: w\models Q}P(w)\]
\(sneezing(bob)\) is true in 3 worlds
\(P(sneezing(bob))=0.7\times 0.8+0.3\times 0.8+0.7\times 0.2=0.94\)
Example Program (ProbLog) Worlds
4 worlds
\[\begin{array}{l} sneezing(X)\leftarrow \mathit{flu}(X),\mathit{flu}\_sneezing(X).\\ sneezing(X)\leftarrow hay\_\mathit{fever}(X),hay\_\mathit{fever}\_sneezing(X).\\ \mathit{flu}(bob).\\ hay\_\mathit{fever}(bob). \end{array}\]
\[\begin{array}{ll} \mathit{flu}\_sneezing(bob).\\ hay\_\mathit{fever}\_sneezing(bob).&hay\_\mathit{fever}\_sneezing(bob).\\ P(w_1)=0.7\times 0.8 &P(w_2)=0.3\times 0.8\\ \mathit{flu}\_sneezing(bob).\\ P(w_3)=0.7\times 0.2 &P(w_4)=0.3\times 0.2 \end{array}\]
\(sneezing(bob)\) is true in 3 worlds
\(P(sneezing(bob))=0.7\times 0.8+0.3\times 0.8+0.7\times 0.2=0.94\)
Logic Programs with Annotated Disjunctions
\[\begin{array}{l} strong\_sneezing(X):0.3\vee moderate\_sneezing(X):0.5\leftarrow \mathit{flu}(X).\\ strong\_sneezing(X):0.2\vee moderate\_sneezing(X):0.6\leftarrow hay\_\mathit{fever}(X).\\ \mathit{flu}(bob).\\ hay\_\mathit{fever}(bob).\\ \end{array}\]
9 worlds
\(P(strong\_sneezing(bob))=?\)
Examples
Throwing coins
heads(Coin):1/2 ; tails(Coin):1/2 :-
toss(Coin),\+biased(Coin).
heads(Coin):0.6 ; tails(Coin):0.4 :-
toss(Coin),biased(Coin).
fair(Coin):0.9 ; biased(Coin):0.1.
toss(coin).Russian roulette with two guns
death:1/6 :- pull_trigger(left_gun).
death:1/6 :- pull_trigger(right_gun).
pull_trigger(left_gun).
pull_trigger(right_gun).Examples
Mendel’s inheritance rules for pea plants
color(X,purple):-cg(X,_A,p).
color(X,white):-cg(X,1,w),cg(X,2,w).
cg(X,1,A):0.5 ; cg(X,1,B):0.5 :-
mother(Y,X),cg(Y,1,A),cg(Y,2,B).
cg(X,2,A):0.5 ; cg(X,2,B):0.5 :-
father(Y,X),cg(Y,1,A),cg(Y,2,B).Probability of paths
path(X,X).
path(X,Y):-path(X,Z),edge(Z,Y).
edge(a,b):0.3.
edge(b,c):0.2.
edge(a,c):0.6.Encoding Bayesian Networks
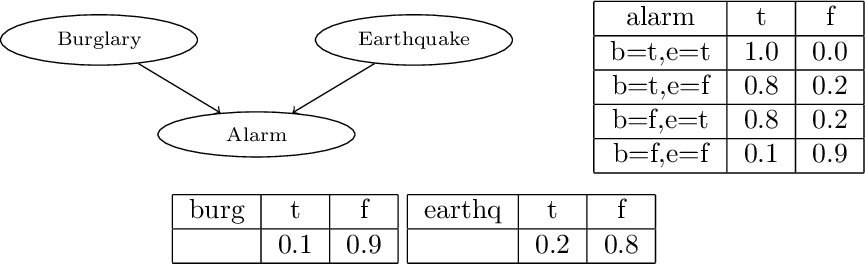
burg(t):0.1 ; burg(f):0.9.
earthq(t):0.2 ; earthq(f):0.8.
alarm(t):-burg(t),earthq(t).
alarm(t):0.8 ; alarm(f):0.2:-burg(t),earthq(f).
alarm(t):0.8 ; alarm(f):0.2:-burg(f),earthq(t).
alarm(t):0.1 ; alarm(f):0.9:-burg(f),earthq(f).PLP Online
http://cplint.lamping.unife.it/
Inference (knwoledge compilation, Monte Carlo)
Parameter learning (EMBLEM)
Structure learning (SLIPCOVER)
https://dtai.cs.kuleuven.be/problog/
Inference (knwoledge compilation, Monte Carlo)
Parameter learning (LFI-ProbLog)
Monty Hall Puzzle
A player is given the opportunity to select one of three closed doors, behind one of which there is a prize.
Behind the other two doors are empty rooms.
Once the player has made a selection, Monty is obligated to open one of the remaining closed doors which does not contain the prize, showing that the room behind it is empty.
He then asks the player if he would like to switch his selection to the other unopened door, or stay with his original choice.
Does it matter if he switches?
Monty Hall Puzzle
:- use_module(library(pita)).
:- endif.
:- pita.
:- begin_lpad.
prize(1):1/3; prize(2):1/3; prize(3):1/3.
selected(1).
open_door(A):0.5; open_door(B):0.5:-
member(A,[1,2,3]), member(B,[1,2,3]),
A<B, \+ prize(A), \+ prize(B),
\+ selected(A), \+ selected(B).
open_door(A):-
member(A,[1,2,3]), \+ prize(A),
\+ selected(A), member(B,[1,2,3]),
prize(B), \+ selected(B).
win_keep:-
selected(A), prize(A).
win_switch:-
member(A,[1,2,3]),
\+ selected(A), prize(A),
\+ open_door(A).
:- end_lpad.Monty Hall Puzzle
Queries:
prob(win_keep,Prob).
prob(win_switch,Prob).Expressive Power
All languages under the distribution semantics have the same expressive power
LPADs have the most general syntax
There are transformations that can convert each one into the others
PRISM, ProbLog to LPAD: direct mapping
LPADs to ProbLog
Clause \(C_i\) with variables \(\overline{X}\) \[H_1:p_1 \vee\ldots\vee H_n:p_n \leftarrow B.\] is translated into \[\begin{array}{l} H_1\leftarrow B,f_{i,1}(\overline{X}).\\ H_2\leftarrow B,not( f_{i,1}(\overline{X})),f_{i,2}(\overline{X}).\\ \vdots\\ H_n\leftarrow B,not(f_{i,1}(\overline{X})),\ldots,not( f_{i,n-1}(\overline{X})).\\ \pi_1::f_{i,1}(\overline{X}).\\ \vdots\\ \pi_{n-1}::f_{i,n-1}(\overline{X}). \end{array}\] where \(\pi_1=p_1\), \(\pi_2=\frac{p_2}{1-\pi_1}\), \(\pi_3=\frac{p_3}{(1-\pi_1)(1-\pi_2)},\ldots\)
In general \(\pi_i=\frac{p_i}{\prod_{j=1}^{i-1}(1-\pi_j)}\)
Conversion to Bayesian Networks
PLP can be converted to Bayesian networks
Conversion for an LPAD \(T\)
For each atom \(A\) in \(H_T\) a binary variable \(A\)
For each clause \(C_i\) in the grounding of \(T\)
\[H_1:p_1 \vee \ldots\vee H_n:p_n \leftarrow B_1, \ldots B_m,\neg {C_1},\ldots,\neg {C_l}\] a variable \(CH_i\) with \(B_1,\ldots,B_m,C_1,\ldots,C_l\) as parents and \(H_1\), \(\ldots\), \(H_n\) and \(null\) as values
Conversion to Bayesian Networks
\[H_1:p_1 \vee \ldots\vee H_n:p_n \leftarrow B_1, \ldots B_m,\neg {C_1},\ldots,\neg {C_l}\]
The CPT of \(CH_i\) is
| \(\ldots\) | \(B_1=1,\ldots,B_m=1,C_1=0,\ldots,C_l=0\) | \(\ldots\) | |
|---|---|---|---|
| \(CH_i=H_1\) | \(0.0\) | \(p_1\) | \(0.0\) |
| \(\ldots\) | |||
| \(CH_i=H_n\) | \(0.0\) | \(p_n\) | \(0.0\) |
| \(CH_i=null\) | \(1.0\) | \(1-\sum_{i=1}^np_i\) | \(1.0\) |
Conversion to Bayesian Networks
Each variable \(A\) corresponding to atom \({A}\) has as parents all the variables \(CH_i\) of clauses \(C_i\) that have \({A}\) in the head.
The CPT for \(A\) is:
| \(\mbox{at least one parent = A}\) | \(\mbox{remaining cols}\) | |
|---|---|---|
| \(A=1\) | 1.0 | 0.0 |
| \(A=0\) | 0.0 | 1.0 |
Conversion to Bayesian Networks
\( \begin{array}{lll} C_1&=&{x1} :0.4\vee {x2}:0.6.\\ C_2&=&{x2}:0.1 \vee {x3}:0.9.\\ C_3&=&{x4}:0.6\vee {x5}:0.4\leftarrow {x1}.\\ C_4&=& {x5}:0.4\leftarrow {x2},{x3}.\\ C_5&=& {x6}:0.3 \vee {x7}:0.2\leftarrow {x2},{x5}. \end{array}\)
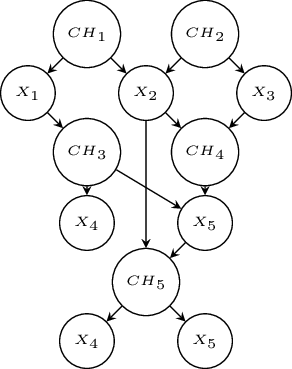
Conversion to Bayesian Networks
| \(CH_1,CH_2\) | \(x1,x2\) | \(x1,x3\) | \(x2,x2\) | \(x2,x3\) |
|---|---|---|---|---|
| \(x2=1\) | 1.0 | 0.0 | 1.0 | 1.0 |
| \(x2=0\) | 0.0 | 1.0 | 0.0 | 0.0 |
| \(x2,x5\) | 1,1 | 1,0 | 0,1 | 0,0 |
|---|---|---|---|---|
| \(CH_5=x6\) | 0.3 | 0.0 | 0.0 | 0.0 |
| \(CH_5=x7\) | 0.2 | 0.0 | 0.0 | 0.0 |
| \(CH_5=null\) | 0.5 | 1.0 | 1.0 | 1.0 |

Function Symbols
What if function symbols are present?
Infinite, countable Herbrand universe
Infinite, countable Herbrand base
Infinite, countable grounding of the program \(T\)
Uncountable \(W_T\)
Each world infinite, countable
\(P(w)=0\)
Semantics not well-defined
Game of dice
on(0,1):1/3 ; on(0,2):1/3 ; on(0,3):1/3.
on(T,1):1/3 ; on(T,2):1/3 ; on(T,3):1/3 :-
T1 is T-1, T1>=0, on(T1,F), \+ on(T1,3).Hidden Markov Models

hmm(S,O):-hmm(q1,[],S,O).
hmm(end,S,S,[]).
hmm(Q,S0,S,[L|O]):-
Q\= end,
next_state(Q,Q1,S0),
letter(Q,L,S0),
hmm(Q1,[Q|S0],S,O).
next_state(q1,q1,_S):1/3;next_state(q1,q2_,_S):1/3;
next_state(q1,end,_S):1/3.
next_state(q2,q1,_S):1/3;next_state(q2,q2,_S):1/3;
next_state(q2,end,_S):1/3.
letter(q1,a,_S):0.25;letter(q1,c,_S):0.25;
letter(q1,g,_S):0.25;letter(q1,t,_S):0.25.
letter(q2,a,_S):0.25;letter(q2,c,_S):0.25;
letter(q2,g,_S):0.25;letter(q2,t,_S):0.25.Description Logics
DISPONTE: “DIstribution Semantics for Probabilistic ONTologiEs” [Riguzzi et al. SWJ15]
Probabilistic axioms:
\(p:: E\)
e.g., \(p:: C\sqsubseteq D\) represents the fact that we believe in the truth of \(C \sqsubseteq D\) with probability \(p\).
DISPONTE applies the distribution semantics of probabilistic logic programming to description logics
DISPONTE
World \(w\): regular DL KB obtained by selecting or not the probabilistic axioms
Probability of a query \(Q\) given a world \(w\): \(P(Q|w)=1\) if \(w\models Q\), 0 otherwise
Probability of \(Q\) \(P(Q)=\sum_w P(Q,w)=\sum_w P(Q|w)P(w)=\sum_{w: w\models Q}P(w)\)
Example
\[\begin{aligned} &&0.4::{\mathit{fluffy}}: Cat\\ &&0.3::tom : Cat \\ &&0.6:: Cat \sqsubseteq Pet \\ &&\exists hasAnimal.Pet \sqsubseteq NatureLover\\ &&(kevin, {\mathit{fluffy}}):hasAnimal \\ &&(kevin, tom):hasAnimal \end{aligned}\]

\(P(kevin:NatureLover)=0.4\times 0.3 \times 0.6+0.4\times 0.6 \times 0.7+ 0.6 \times 0.3\times 0.6 =0.348\)
Knowledge-Based Model Construction
The probabilistic logic theory is used directly as a template for generating an underlying complex graphical model [Breese et al. TSMC94].
Languages: CLP(BN), Markov Logic
CLP(BN) [Costa UAI02]
Variables in a CLP(BN) program can be random
Their values, parents and CPTs are defined with the program
To answer a query with uninstantiated random variables, CLP(BN) builds a BN and performs inference
The answer will be a probability distribution for the variables
Probabilistic dependencies expressed by means of CLP constraints
{ Var = Function with p(Values, Dist) }
{ Var = Function with p(Values, Dist, Parents) }CLP(BN)
....
course_difficulty(Key, Dif) :-
{ Dif = difficulty(Key) with p([h,m,l],
[0.25, 0.50, 0.25]) }.
student_intelligence(Key, Int) :-
{ Int = intelligence(Key) with p([h, m, l],
[0.5,0.4,0.1]) }.
....
registration(r0,c16,s0).
registration(r1,c10,s0).
registration(r2,c57,s0).
registration(r3,c22,s1).CLP(BN)
....
registration_grade(Key, Grade):-
registration(Key, CKey, SKey),
course_difficulty(CKey, Dif),
student_intelligence(SKey, Int),
{ Grade = grade(Key) with
p([a,b,c,d],
%h h h m h l m h m m m l l h l m l l
[0.20,0.70,0.85,0.10,0.20,0.50,0.01,0.05,0.10,
0.60,0.25,0.12,0.30,0.60,0.35,0.04,0.15,0.40,
0.15,0.04,0.02,0.40,0.15,0.12,0.50,0.60,0.40,
0.05,0.01,0.01,0.20,0.05,0.03,0.45,0.20,0.10 ],
[Int,Dif]))
}.
.....CLP(BN)
?- [school_32].
?- registration_grade(r0,G).
p(G=a)=0.4115,
p(G=b)=0.356,
p(G=c)=0.16575,
p(G=d)=0.06675 ?
?- registration_grade(r0,G),
student_intelligence(s0,h).
p(G=a)=0.6125,
p(G=b)=0.305,
p(G=c)=0.0625,
p(G=d)=0.02 ?Markov Networks
Undirected graphical models
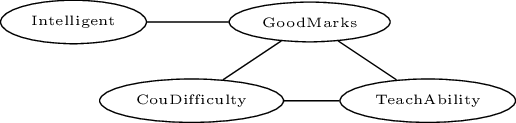 \(\phi_i\)
\(\phi_i\)
\[\begin{aligned} P(\mathbf{x})&=&\frac{\prod_i\phi_i(\mathbf{x_i})}{Z}\\ Z&=&\sum_{\mathbf{x}}\prod_i\phi_i(\mathbf{x_i})\end{aligned}\]
| Intelligent | GoodMarks | \(\phi_i(I,G)\) | |
|---|---|---|---|
| false | false | 4.5 | |
| false | true | 4.5 | |
| true | false | 1.0 | |
| true | true | 4.5 |
Markov Networks

If all the potential are strictly positive, we can use a log-linear model (where the \(f_i\)s are features)
\( \begin{array}{c} P(\mathbf{x})=\frac{\exp({\sum_i w_i f_i(\mathbf{x_i})})}{Z}\\ Z=\sum_{\mathbf{x}}\exp({\sum_i w_i f_i(\mathbf{x_i})}))\\ f_i(Intelligent, GoodMarks)=\left\{ \begin{array}{ll} 1 &\mbox{if $\neg$Intelligent$\vee$GoodMarks}\\ 0 & \mbox{otherwise} \end{array}\right.\\ w_i=1.5 \end{array}\)
Markov Logic
A Markov Logic Network (MLN) [Richardson, Domingos ML06] is a set of pairs \((F, w)\) where \(F\) is a formula in first-order logic \(w\) is a real number
Together with a set of constants, it defines a Markov network with
One node for each grounding of each predicate in the MLN
One feature for each grounding of each formula \(F\) in the MLN, with the corresponding weight \(w\)
Markov Logic Example
\[\begin{array}{ll} 1.5 &\forall x\ Intelligent(x)\rightarrow GoodMarks(x)\\ 1.1&\forall x,y\ Friends(x,y)\rightarrow (Intelligent(x)\leftrightarrow Intelligent(y)) \end{array}\]
Constants Anna (A) and Bob (B)

Markov Networks
Probability of an interpretation \(\mathbf{x}\) \[P(\mathbf{x})=\frac{\exp({\sum_i w_i n_i(\mathbf{x_i})})}{Z}\]
\(n_i(\mathbf{x_i})=\) number of true groundings of formula \(F_i\) in \(\mathbf{x}\)
Typed variables and constants greatly reduce size of ground Markov net
Reasoning Tasks
Inference: we want to compute the probability of a query given the model and, possibly, some evidence
Weight learning: we know the structural part of the model (the logic formulas) but not the numeric part (the weights) and we want to infer the weights from data
Structure learning we want to infer both the structure and the weights of the model from data
Applications
Link prediction: given a (social) network, compute the probability of the existence of a link between two entities (UWCSE)
advisedby(X, Y) :0.7 :-
publication(P, X),
publication(P, Y),
student(X).Applications
Classify web pages on the basis of the link structure (WebKB)
coursePage(Page1): 0.3 :- linkTo(Page2,Page1),coursePage(Page2).
coursePage(Page1): 0.6 :- linkTo(Page2,Page1),facultyPage(Page2).
...
coursePage(Page): 0.9 :- has('syllabus',Page).
...Applications
Entity resolution: identify identical entities in text or databases

samebib(A,B):0.9 :-
samebib(A,C), samebib(C,B).
sameauthor(A,B):0.6 :-
sameauthor(A,C), sameauthor(C,B).
sametitle(A,B):0.7 :-
sametitle(A,C), sametitle(C,B).
samevenue(A,B):0.65 :-
samevenue(A,C), samevenue(C,B).
samebib(B,C):0.5 :-
author(B,D),author(C,E),sameauthor(D,E).
samebib(B,C):0.7 :-
title(B,D),title(C,E),sametitle(D,E).
samebib(B,C):0.6 :-
venue(B,D),venue(C,E),samevenue(D,E).
samevenue(B,C):0.3 :-
haswordvenue(B,logic),
haswordvenue(C,logic).
...Applications
Chemistry: given the chemical composition of a substance, predict its mutagenicity or its carcenogenicity
active(A):0.4 :-
atm(A,B,c,29,C),
gteq(C,-0.003),
ring_size_5(A,D).
active(A):0.6:-
lumo(A,B), lteq(B,-2.072).
active(A):0.3 :-
bond(A,B,C,2),
bond(A,C,D,1),
ring_size_5(A,E).
active(A):0.7 :-
carbon_6_ring(A,B).
active(A):0.8 :-
anthracene(A,B).
...Applications
Medicine: diagnose diseases on the basis of patient information (Hepatitis), influence of genes on HIV, risk of falling of elderly people


Inference for PLP under DS
Computing the probability of a query (no evidence)
Knowledge compilation:
compile the program to an intermediate representation
Binary Decision Diagrams (BDD) (ProbLog [De Raedt et al. IJCAI07],
cplint[Riguzzi AIIA07,Riguzzi LJIGPL09], PITA [Riguzzi & Swift ICLP10])deterministic, Decomposable Negation Normal Form circuit (d-DNNF) (ProbLog2 [Fierens et al. TPLP15])
Sentential Decision Diagrams
compute the probability by weighted model counting
Inference for PLP under DS
Bayesian Network based:
Convert to BN
Use BN inference algorithms (CVE [Meert et al. ILP09])
Lifted inference
Knowledge Compilation
Assign Boolean random variables to the probabilistic rules
Given a query \(Q\), compute its explanations, assignments to the random variables that are sufficient for entailing the query
Let \(K\) be the set of all possible explanations
Build a Boolean formula \(F(Q)\)
Build a BDD representing \(F(Q)\)
ProbLog
\[\begin{array}{l} sneezing(X)\leftarrow \mathit{flu}(X),\mathit{flu}\_sneezing(X).\\ sneezing(X)\leftarrow hay\_\mathit{fever}(X),hay\_\mathit{fever}\_sneezing(X).\\ \mathit{flu}(bob).\\ hay\_\mathit{fever}(bob).\\ 0.7::\mathit{flu}\_sneezing(X).\\ 0.8::hay\_\mathit{fever}\_sneezing(X).\\ \end{array}\]
Definitions
Composite choice \(\kappa\): consistent set of atomic choices \((C_i,\theta_j,l)\) with \(l\in\{1,2\}\)
Set of worlds compatible with \(\kappa\): \(\omega_\kappa=\{w_\sigma|\kappa \subseteq \sigma\}\)
Explanation \(\kappa\) for a query \(Q\): \(Q\) is true in every world of \(\omega_\kappa\)
A set of composite choices \(K\) is covering with respect to \(Q\): every world \(w\) in which \(Q\) is true is such that \(w\in\omega_K\) where \(\omega_K=\bigcup_{\kappa\in K}\omega_\kappa\)
Example: \[\label{expls} K_1=\{\{(C_1,\{X/bob\},1)\},\{(C_2,\{X/bob\},1)\}\}\] is covering for \(sneezing(bob)\).
Finding Explanations
All explanations for the query are collected
ProbLog: source to source transformation for facts, use of dynamic database
cplint(PITA): source to source transformation, addition of an argument to predicates
Explanation Based Inference Algorithm
\(K=\) set of explanations found for \(Q\), the probability of \(Q\) is given by the probability of the formula \[f_K(\mathbf{X})=\bigvee_{\kappa\in K}\bigwedge_{(C_i,\theta_j,l)\in\kappa}(X_{C_i\theta_j}=l)\] where \(X_{C_i\theta_j}\) is a random variable whose domain is \({1,2}\) and \(P(X_{C_i\theta_j}=l)=P_0(C_i,l)\)
Binary domain: we use a Boolean variable \(X_{ij}\) to represent \((X_{C_i\theta_j}=1)\)
\(\overline{X_{ij}}\) represents \((X_{C_i\theta_j}=2)\)
Example
A set of covering explanations for \( sneezing(bob) \) is \(K=\{\kappa_1,\kappa_2\}\)
\(\kappa_1=\{(C_1,\{X/bob\},1)\}\) \(\kappa_2=\{(C_2,\{X/bob\},1)\}\)
\(K=\{\kappa_1,\kappa_2\}\)
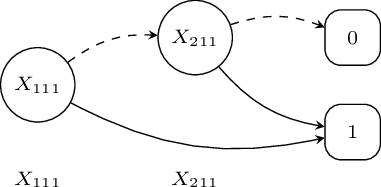
\(f_{K}(\mathbf{X})=(X_{C_1\{X/bob\}}=1)\vee (X_{C_2\{X/bob\}}=1)\).
\(X_{11}=(X_{C_1\{X/bob\}}=1)\) \(X_{21}=(X_{C_2\{X/bob\}}=1)\)
\(f_{K}(\mathbf{X})=X_{11}\vee X_{21}\).
\(P(f_{K}(\mathbf{X}))=P(X_{11}\vee X_{21})=P(X_{11})+P(X_{21})-P(X_{11})P(X_{21})\)
In order to compute the probability, we must make the explanations mutually exclusive
[De Raedt at. IJCAI07]: Binary Decision Diagram (BDD)
Binary Decision Diagrams
A BDD for a function of Boolean variables is a rooted graph that has one level for each Boolean variable
A node \(n\) in a BDD has two children: one corresponding to the 1 value of the variable associated with \(n\) and one corresponding the 0 value of the variable
The leaves store either 0 or 1.

Binary Decision Diagrams
BDDs can be built by combining simpler BDDs using Boolean operators
While building BDDs, simplification operations can be applied that delete or merge nodes
Merging is performed when the diagram contains two identical sub-diagrams
Deletion is performed when both arcs from a node point to the same node
A reduced BDD often has a much smaller number of nodes with respect to the original BDD
Binary Decision Diagrams

\[f_K(\mathbf{X})=X_{11}\times f_K^{X_{11}}(\mathbf{X})+\neg X_{11}\times f_K^{\neg X_{11}}(\mathbf{X})\]
\[P(f_K(\mathbf{X}))=P(X_{11})P(f_K^{X_{11}}(\mathbf{X}))+(1-P(X_{11}))P(f_K^{\neg X_1}(\mathbf{X}))\]
\[P(f_K(\mathbf{X}))=0.7\cdot P(f_K^{X_{11}}(\mathbf{X}))+0.3\cdot P(f_K^{\neg X_{11}}(\mathbf{X}))\]
Probability from a BDD
Dynamic programming algorithm [De Raedt et al IJCAI07]
Initialize map \(p\)
Call \(\mathrm{Prob}(root)\)
Function \(\mathrm{Prob}(n)\)
if \(p(n)\) exists, return \(p(n)\)
if \(n\) is a terminal note
return \(value(n)\)
else
\(prob:=\mathrm{Prob}(child_1(n)\times p(v(n))+\mathrm{Prob}(child_0(n))\times (1-p(v(n)))\)
Add \((n,prob)\) to \(p\), return \(prob\)
Logic Programs with Annotated Disjunctions
\[\begin{array}{llll} C_1=&strong\_sneezing(X):0.3\vee moderate\_sneezing(X):0.5&\leftarrow& flu(X).\\ C_2=&strong\_sneezing(X):0.2\vee moderate\_sneezing(X):0.6&\leftarrow& hay\_fever(X).\\ C_3=&flu(bob).\\ C_4=&hay\_fever(bob).\\ \end{array}\]
Distributions over the head of rules
More than two head atoms
Example
A set of covering explanations for \( strong\_sneezing(bob) \) is \(K=\{\kappa_1,\kappa_2\}\)
\(\kappa_1=\{(C_1,\{X/bob\},1)\}\)
\(\kappa_2=\{(C_2,\{X/bob\},1)\}\)
\(K=\{\kappa_1,\kappa_2\}\)
\(X_{11}=X_{C_1\{X/bob\}}\)
\(X_{21}=X_{C_2\{X/bob\}}\)
\(f_{K}(\mathbf{X})=(X_{11}=1)\vee (X_{21}=1)\).
\(P(f_{X})=P(X_{11}=1)+P(X_{21}=1)-P(X_{11}=1)P(X_{21}=1)\)
To make the explanations mutually exclusive: Multivalued Decision Diagram (MDD)
Multivalued Decision Diagrams

\[f_K(\mathbf{X})=\bigvee_{l \in|X_{11}|}(X_{11}=l)\wedge f_K^{X_{11}=l}(\mathbf{X})\]
\[P(f_K(\mathbf{X}))=\sum_{l \in|X_{11}|}P(X_{11}=l)P(f_K^{X_{11}=l}(\mathbf{X}))\]
\[f_K(\mathbf{X})=(X_{11}=1)\wedge f_K^{X_{11}=1}(\mathbf{X})+(X_{11}=2)\wedge f_K^{X_{11}=2}(\mathbf{X})+(X_{11}=3)\wedge f_K^{X_{11}=3}(\mathbf{X})\]
\[f_K(\mathbf{X})=0.3\cdot P(f_K^{X_{11}=1}(\mathbf{X}))+0.5\cdot P(f_K^{X_{11}=2}(\mathbf{X}))+0.2\cdot P(f_K^{X_{11}=3}(\mathbf{X}))\]
Manipulating Multivalued Decision Diagrams
Use an MDD package
Convert to BDD, use a BDD package: BDD packages more developed, more efficient
Conversion to BDD
Log encoding
Binary splits: more efficient
Transformation to a Binary Decision Diagram
For a variable \(X_{ij}\) having \(n\) values, we use \(n-1\) Boolean variables \(X_{ij1},\ldots,X_{ijn-1}\)
\(X_{ij}=l\) for \(l=1,\ldots n-1\): \(\overline{X_{ij1}}\wedge\overline{X_{ij2}}\wedge\ldots \wedge \overline{X_{ijl-1}}\wedge X_{ijl}\),
\(X_{ij}=n\): \(\overline{X_{ij1}}\wedge\overline{X_{ij2}}\wedge\ldots \wedge\overline{X_{ijn-1}}\).
Parameters: \(P(X_{ij1})=P(X_{ij}=1)\ldots P(X_{ijl})=\frac{P(X_{ij}=l)}{\prod_{m=1}^{l-1}(1-P(X_{ijm}))}\).
Approximate Inference
Inference problem is #P hard
For large models inference is intractable
Approximate inference
Monte Carlo: draw samples of the truth value of the query
Iterative deepening: gives a lower and an upper bound
Compute only the best \(k\) explanations: branch and bound, gives a lower bound
Monte Carlo
The disjunctive clause
\(C_r=H_1:\alpha_1\vee \ldots\vee H_n:\alpha_n\leftarrow L_1,\ldots,L_m.\)
is transformed into the set of clauses \(MC(C_r)\)
\(\begin{array}{l} MC(C_r,1)=H_1\leftarrow L_1,\ldots,L_m,sample\_head(n,r,VC,NH),NH=1.\\ \ldots\\ MC(C_r,n)=H_n\leftarrow L_1,\ldots,L_m,sample\_head(n,r,VC,NH),NH=n.\\ \end{array}\)
Sample truth value of query
Q:... (call(Q)-> NT1 is NT+1 ; NT1 =NT), ...
Inference in DISPONTE
The probability of a query \(Q\) can be computed according to the distribution semantics by first finding the explanations for \(Q\) in the knowledge base
Explanation: subset of axioms of the KB that is sufficient for entailing \(Q\)
All the explanations for \(Q\) must be found, corresponding to all ways of proving \(Q\)
Inference in DISPONTE
Probability of \(Q\) \(\rightarrow\) probability of the DNF formula \[F(Q)= \bigvee_{e\in E_Q} ( \bigwedge_{F_i \in e} X_{i} )\] where \(E_Q\) is the set of explanations and \(X_i\) is a Boolean random variable associated to axiom \(F_i\)
Binary Decision Diagrams for efficiently computing the probability of the DNF formula
Example
\[\begin{aligned} &&E_1=0.4::{\mathit{fluffy}}: Cat\\ &&E_2=0.3::tom : Cat\\ &&E_3=0.6:: Cat \sqsubseteq Pet\\ &&\exists hasAnimal.Pet \sqsubseteq NatureLover\\ &&(kevin, {\mathit{fluffy}}):hasAnimal \\ &&(kevin, tom):hasAnimal \end{aligned}\]

\(Q=kevin:NatureLover\) has two explanations:
{ (\(E_1\)), (\(E_3\)) }
{ (\(E_2\)), (\(E_3\)) }\(P(Q)=0.4\times 0.6 \times(1-0.3) + 0.3 \times 0.6 =0.348\)
BUNDLE
Binary decision diagrams for Uncertain reasoNing on Description Logic thEories [Riguzzi et al. SWJ15]
BUNDLE performs inference over DISPONTE knowledge bases.
It exploits an underlying ontology reasoner able to return all explanations for a query, such as Pellet [Sirin et al, WS 2007]
Then DNF formula built and converted to BDDs for computing the probability
TRILL
Tableau Reasoner for descrIption Logics in proLog
TRILL implements the tableau algorithm using Prolog
It resolves the axiom pinpointing problem in which we are interested in the set of explanations that entail a query
It returns the set of the explanations
It can build BDDs encoding the set of explanations and return the probability
TRILL
Available online at http://trill.lamping.unife.it/
Pets example http://trill.lamping.unife.it/trill_on_swish/example/peoplePets.owl
Parameter Learning
Problem: given a set of interpretations, a program, find the parameters maximizing the likelihood of the interpretations (or of instances of a target predicate)
The interpretations record the truth value of ground atoms, not of the choice variables
Unseen data: relative frequency can’t be used
Parameter Learning
An Expectation-Maximization algorithm must be used:
Expectation step: the distribution of the unseen variables in each instance is computed given the observed data
Maximization step: new parameters are computed from the distributions using relative frequency
End when likelihood does not improve anymore
Parameter Learning
[Thon et al. ECML 2008] proposed an adaptation of EM for CPT-L, a simplified version of LPADs
The algorithm computes the counts efficiently by repeatedly traversing the BDDs representing the explanations
[Ishihata et al. ILP 2008] independently proposed a similar algorithm
LFI-ProbLog [Gutamnn et al. ECML 2011]: EM for ProbLog
EMBLEM [Riguzzi & Bellodi IDA 2013] adapts [Ishihata et al. ILP 2008] to LPADs
EMBLEM
EM over Bdds for probabilistic Logic programs Efficient Mining
Input: an LPAD; logical interpretations (data); target predicate(s)
all ground atoms in the interpretations for the target predicate(s) correspond to as many queries
BDDs encode the explanations for each query \(Q\)
Expectations computed with two passes over the BDDs
EDGE
Em over bDds for description loGics paramEter learning
EDGE is inspired to EMBLEM [Bellodi and Riguzzi, IDA 2013]
Takes as input a DL theory and a number of examples that represent queries.
The queries are concept assertions and are divided into:
positive examples;
negative examples.
EDGE computes the explanations of each example using BUNDLE, that builds the corresponding BDD.
For negative examples, EDGE computes the explanations of the query, builds the BDD and then negates it.
Structure Learning for LPADs
Given a trivial LPAD or an empty one, a set of interpretations (data)
Find the model and the parameters that maximize the probability of the data (log-likelihood)
SLIPCOVER: Structure LearnIng of Probabilistic logic program by searching OVER the clause space EMBLEM [Riguzzi & Bellodi TPLP 2015]
Beam search in the space of clauses to find the promising ones
Greedy search in the space of probabilistic programs guided by the LL of the data.
Parameter learning by means of EMBLEM
SLIPCOVER
Cycle on the set of predicates that can appear in the head of clauses, either target or background
For each predicate, beam search in the space of clauses
The initial set of beams is generated by building a set of bottom clauses as in Progol [Muggleton NGC 1995]
Mode Declarations
Syntax
modeh(RecallNumber,PredicateMode).
modeb(RecallNumber,PredicateMode).RecallNumbercan be a number or *. Usually *. Maximum number of answers to queries to include in the bottom clausePredicateMode: template of the form:
p(ModeType, ModeType,...) Mode Declarations
ModeTypecan be:Simple:
+Tinput variables of typeT;-Toutput variables of typeT; or#T,-#Tconstants of typeT.
Structured: of the form
f(..)wherefis a function symbol and every argument can be either simple or structured.
Mode Declarations
Some examples:
modeb(1,mem(+number,+list)).
modeb(1,dec(+integer,-integer)).
modeb(1,mult(+integer,+integer,-integer)).
modeb(1,plus(+integer,+integer,-integer)).
modeb(1,(+integer)=(#integer)).
modeb(*,has_car(+train,-car))
modeb(1,mem(+number,[+number|+list])). Bottom Clause \(\bot\)
Most specific clause covering an example \(e\)
Form: \(e\leftarrow B\)
\(B\): set of ground literals that are true regarding the example \(e\)
\(B\) obtained by considering the constants in \(e\) and querying the predicates of the background for true atoms regarding these constants
A map from types to lists of constants is kept, it is enlarged with constants in the answers to the queries and the procedure is iterated a user-defined number of times
Values for output arguments are used as input arguments for other predicates
Bottom Clause \(\bot\)
Initialize to empty a map \(m\) from types to lists of values
Pick a \(modeh(r,s)\), an example \(e\) matching \(s\), add to \(m(T)\) the values of \(+T\) arguments in \(e\)
For \(i=1\) to \(d\)
For each \(modeb(r,s)\)
Bottom Clause \(\bot\)
For each possible way of building a query \(q\) from \(s\) by replacing \(+T\) and \(\#T\) arguments with constants from \(m(T)\) and all other arguments with variables
Find all possible answers for \(q\) and put them in a list \(L\)
\(L':=\) \(r\) elements sampled from \(L\)
For each \(l\in L'\), add the values in \(l\) corresponding to \(-T\) or \(-\#T\) to \(m(T)\)
Bottom Clause \(\bot\)
Example:
\(e=father(john,mary)\)
\(B=\{parent(john,mary), parent(david,steve),\)
\(parent(kathy,mary), female(kathy),male(john), male(david)\}\)
\(modeh(father(+person,+person)).\)
\(modeb(parent(+person,-person)).\) \(modeb(parent(-\#person,+person)).\)
\(modeb(male(+person)).\) \(modeb(female(\#person)).\)
\(e\leftarrow B=father(john,mary)\leftarrow parent(john,mary),male(john),\)
\(parent(kathy,mary),female(kathy).\)
Bottom Clause \(\bot\)
The resulting ground clause \(\bot\) is then processed by replacing each term in a + or - placemarker with a variable
An input variable (+T) must appear as an output variable with the same type in a previous literal and a constant (#T or -#T) is not replaced by a variable.
\(\bot=father(X,Y)\leftarrow parent(X,Y),male(X),parent(kathy,Y),female(kathy).\)
SLIPCOVER
The initial beam associated with predicate \(P/Ar\) will contain the clause with the empty body \(h:0.5.\) for each bottom clause \(h\ {:\!-}\ b_1,\ldots,b_m\)
In each iteration of the cycle over predicates, it performs a beam search in the space of clauses for the predicate.
The beam contains couples \((Cl, LIterals)\) where \(Literals=\{b_1,\ldots,b_m\}\)
For each clause \(Cl\) of the form \(Head \ {:\!-}\ Body\), the refinements are computed by adding a literal from \(Literals\) to the body.
SLIPCOVER
The tuple (\(Cl'\), \(Literals'\)) indicates a refined clause \(Cl'\) together with the new set \(Literals'\)
EMBLEM is then executed for a theory composed of the single refined clause.
LL is used as the score of the updated clause \((Cl'',Literals')\).
\((Cl'',Literals')\) is then inserted into a list of promising clauses.
Two lists are used, \(TC\) for target predicates and \(BC\) for background predicates.
These lists ave a maximum size
SLIPCOVER
After the clause search phase, SLIPCOVER performs a greedy search in the space of theories:
it starts with an empty theory and adds a target clause at a time from the list \(TC\).
After each addition, it runs EMBLEM and computes the LL of the data as the score of the resulting theory.
If the score is better than the current best, the clause is kept in the theory, otherwise it is discarded.
Finally, SLIPCOVER adds all the clauses in \(BC\) to the theory and performs parameter learning on the resulting theory.
Experiments - Area Under the PR Curve
| System | HIV | UW-CSE | Mondial | ||
|---|---|---|---|---|---|
| SLIPCOVER | \(0.82 \pm0.05\) | \(0.11\pm 0.08\) | \(0.86 \pm 0.07\) | ||
| SLIPCASE | \(0.78\pm0.05\) | \(0.03\pm 0.01\) | \(0.65 \pm 0.06\) | ||
| LSM | \(0.37\pm0.03\) | \(0.07\pm0.02\) | - | ||
| ALEPH++ | - | \(0.05\pm0.01\) | \(0.87 \pm 0.07\) | ||
| RDN-B | \(0.28 \pm 0.06\) | \(0.28 \pm 0.06\) | \(0.77 \pm 0.07\) | ||
| MLN-BT | \(0.29 \pm 0.04\) | \(0.18 \pm 0.07\) | \(0.74 \pm 0.10\) | ||
| MLN-BC | \(0.51 \pm 0.04\) | \(0.06 \pm 0.01\) | \(0.59 \pm 0.09\) | ||
| BUSL | \(0.38 \pm 0.03\) | \(0.01 \pm 0.01\) | - |
Experiments - Area Under the PR Curve
| System | Carcinogenesis | Mutagenesis | Hepatitis | ||
|---|---|---|---|---|---|
| SLIPCOVER | \(0.60\) | \(0.95\pm0.01\) | \(0.80\pm0.01\) | ||
| SLIPCASE | \(0.63\) | \(0.92\pm 0.08\) | \(0.71\pm0.05\) | ||
| LSM | - | - | \(0.53\pm 0.04\) | ||
| ALEPH++ | \(0.74\) | \(0.95\pm0.01\) | - | ||
| RDN-B | \(0.55\) | \(0.97 \pm 0.03\) | \(0.88 \pm 0.01\) | ||
| MLN-BT | \(0.50\) | \(0.92 \pm 0.09\) | \(0.78 \pm 0.02\) | ||
| MLN-BC | \(0.62\) | \(0.69 \pm 0.20\) | \(0.79 \pm 0.02\) | ||
| BUSL | - | - | \(0.51 \pm 0.03\) |
Bongard Problems
Introduced by the Russian scientist M. Bongard
Pictures, some positive and some negative
Problem: discriminate between the two classes.
The pictures contain shapes with different properties, such as small, large, pointing down, … and different relationships between them, such as inside, above, …

Input File
Preamble
:-use_module(library(slipcover)).
:- if(current_predicate(use_rendering/1)).
:- use_rendering(c3).
:- use_rendering(lpad).
:- endif.
:-sc.
:- set_sc(megaex_bottom,20).
:- set_sc(max_iter,3).
:- set_sc(max_iter_structure,10).
:- set_sc(maxdepth_var,4).
:- set_sc(verbosity,1).See http://cplint.lamping.unife.it/help/help-cplint.html for a list of options
Input File
Theory for parameter learning and background
bg([]).
in([
(pos:0.5 :-
circle(A),
in(B,A)),
(pos:0.5 :-
circle(A),
triangle(B))]).Input File
Data: two formats, models
begin(model(2)).
pos.
triangle(o5).
config(o5,up).
square(o4).
in(o4,o5).
circle(o3).
triangle(o2).
config(o2,up).
in(o2,o3).
triangle(o1).
config(o1,up).
end(model(2)).
begin(model(3)).
neg(pos).
circle(o4).
circle(o3).
in(o3,o4).
....Input File
Data: two formats, keys (internal representation)
pos(2).
triangle(2,o5).
config(2,o5,up).
square(2,o4).
in(2,o4,o5).
circle(2,o3).
triangle(2,o2).
config(2,o2,up).
in(2,o2,o3).
triangle(2,o1).
config(2,o1,up).
neg(pos(3)).
circle(3,o4).
circle(3,o3).
in(3,o3,o4).
square(3,o2).
circle(3,o1).
in(3,o1,o2).
....Input File
Folds
Target predicates:
output(<predicate>)Input predicates are those whose atoms you are not interested in predicting
input_cw(<predicate>/<arity>).True atoms are those in the interpretations and those derivable from them using the background knowledge
Open world input predicates are declared with
input(<predicate>/<arity>).the facts in the interpretations, the background clauses and the clauses of the input program are used to derive atoms
Input File
fold(train,[2,3,5,...]).
fold(test,[490,491,494,...]).
output(pos/0).
input_cw(triangle/1).
input_cw(square/1).
input_cw(circle/1).
input_cw(in/2).
input_cw(config/2).Input File
Language bias
\(determination(p/n,q/m)\): atoms for \(q/m\) can appear in the body of rules for \(p/n\)
determination(pos/0,triangle/1).
determination(pos/0,square/1).
determination(pos/0,circle/1).
determination(pos/0,in/2).
determination(pos/0,config/2).
modeh(*,pos).
modeb(*,triangle(-obj)).
modeb(*,square(-obj)).
modeb(*,circle(-obj)).
modeb(*,in(+obj,-obj)).
modeb(*,in(-obj,+obj)).
modeb(*,config(+obj,-#dir)).Input File
Search bias
lookahead(logp(B),[(B=_C)]).Bongard Problems
Parameter learning
induce_par([train],P),
test(P,[test],LL,AUCROC,ROC,AUCPR,PR).Structure learning
induce([train],P),
test(P,[test],LL,AUCROC,ROC,AUCPR,PR).Exercise
Write SLIPCOVER input file for
University Database http://www.cs.sfu.ca/~oschulte/jbn/dataset.html Data university.pl
Mutagenesis http://www.doc.ic.ac.uk/~shm/mutagenesis.html Data muta.pl
Conclusions
Exciting field!
Much is left to do:
Lifted inference
Continuous variables
Structure learning search strategies

References
Bellodi, E. and Riguzzi, F. (2012). Learning the structure of probabilistic logic programs. In Inductive Logic Programming 21st International Conference, ILP 2011, London, UK, July 31 - August 3, 2011. Revised Papers, volume 7207 of LNCS, pages 61-75, Heidelberg, Germany. Springer.
Bellodi, E. and Riguzzi, F. (2013). Expectation Maximization over binary decision diagrams for probabilistic logic programs. Intelligent Data Analysis, 17(2).
Breese, J. S., Goldman, R. P., and Wellman, M. P. (1994). Introduction to the special section on knowledge-based construction of probabilistic and decision models. IEEE Transactions On Systems, Man and Cybernetics, 24(11):1577-1579.
References
Dantsin, E. (1991). Probabilistic logic programs and their semantics. In Russian Conference on Logic Programming, volume 592 of LNCS, pages 152-164. Springer.
De Raedt, L., Kimmig, A., and Toivonen, H. (2007). Problog: A probabilistic prolog and its application in link discovery. In International Joint Conference on Artificial Intelligence, pages 2462-2467.
Fierens, D., den Broeck, G.V., Renkens, J., Shterionov, D.S., Gutmann, B., Thon, I., Janssens, G., De Raedt, L.: Inference and learning in probabilistic logic pro- grams using weighted boolean formulas. Theory and Practice of Logic Program- ming 15(3), 358-401 (2015)
References
Gutmann, B., Thon, I., and Raedt, L. D. (2011). Learning the parameters of probabilistic logic programs from interpretations. In European Conference on Machine Learning and Knowledge Discovery in Databases, volume 6911 of LNCS, pages 581-596. Springer.
Ishihata, M., Kameya, Y., Sato, T., and Minato, S. (2008). Propositionalizing the em algorithm by bdds. In Late Breaking Papers of the 18th International Conf. on Inductive Logic Programming, pages 44-49.
Meert, W., Struyf, J., and Blockeel, H. (2009). CP-Logic theory inference with contextual variable elimination and comparison to bdd based inference methods. In ILP 2009.
References
Meert, W., Taghipour, N., and Blockeel, H. (2010). First-order bayes-ball. In Balcázar, J. L., Bonchi, F., Gionis, A., and Sebag, M., editors, Machine Learning and Knowledge Discovery in Databases, European Conference, ECML PKDD 2010, Barcelona, Spain, September 20-24, 2010, Proceedings, Part II, volume 6322 of Lecture Notes in Computer Science, pages 369-384. Springer.
Muggleton, S. (1995). Inverse entailment and progol. New Generation Comput., 13(3&4):245-286.
Poole, D. (1993). Logic programming, abduction and probability - a top-down anytime algorithm for estimating prior and posterior probabilities. New Gener. Comput., 11(3):377-400.
Poole, D. (1997). The Independent Choice Logic for modelling multiple agents under uncertainty. Artif. Intell., 94(1-2):7-56.
References
Riguzzi, F. (2007). A top down interpreter for LPAD and CP-logic. In Congress of the Italian Association for Artificial Intelligence, number 4733 in LNAI, pages 109-120. Springer.
Riguzzi, F. (2009). Extended semantics and inference for the Independent Choice Logic. Logic Journal of the IGPL.
Riguzzi, F. and Swift, T. (2010). Tabling and Answer Subsumption for Reasoning on Logic Programs with Annotated Disjunctions. In Hermenegildo, M. and Schaub, T., editors, Technical Communications of the 26th Int’l. Conference on Logic Programming (ICLP10), volume 7 of Leibniz International Proceedings in Informatics (LIPIcs), pages 162-171, Dagstuhl, Germany. Schloss Dagstuhl-Leibniz-Zentrum fuer Informatik.
References
Sato, T. (1995). A statistical learning method for logic programs with distribution semantics. In International Conference on Logic Programming, pages 715-729.
Shachter, R. D. (1998). Bayes-ball: The rational pastime (for determining irrelevance and requisite information in belief networks and influence diagrams. In In Uncertainty in Artificial Intelligence, pages 480-487. Morgan Kaufmann.
Thon, I., Landwehr, N., and Raedt, L. D. (2008). A simple model for sequences of relational state descriptions. In Daelemans, W., Goethals, B., and Morik, K., editors, Machine Learning and Knowledge Discovery in Databases, European Conference, ECML/PKDD 2008, Antwerp, Belgium, September 15-19, 2008, Proceedings, Part II, volume 5212 of Lecture Notes in Computer Science, pages 506-521. Springer.
References
Vennekens, J., Verbaeten, S., and Bruynooghe, M. (2004). Logic programs with annotated disjunctions. In International Conference on Logic Programming, volume 3131 of LNCS, pages 195-209. Springer.
Breese, J. S., Goldman, R. P., and Wellman, M. P. (1994). Introduction to the special section on knowledge-based construction of probabilistic and decision models. IEEE Transactions On Systems, Man and Cybernetics, 24(11):1577-1579.
Costa, Vitor Santos, et al. CLP(BN): Constraint logic programming for probabilistic knowledge. Proceedings of the Nineteenth conference on Uncertainty in Artificial Intelligence. Morgan Kaufmann Publishers Inc., 2002.
Richardson, Matthew, and Pedro Domingos. Markov logic networks. Machine learning 62.1-2 (2006): 107-136.
References
Riguzzi, Fabrizio, et al. “Probabilistic description logics under the distribution semantics.” Semantic Web 6.5 (2015): 477-501.